Complex analysis, as we usually learn it, is the study of differentiable functions from $\mathbb{C}$ to $\mathbb{C}$. These functions have many nice properties: if they are differentiable even once then they are infinitely differentiable; in fact they are analytic, meaning they can be represented in the vicinity of any point as an absolutely convergent power series; moreover at any point $z_0$, the power series has radius of convergence equal to the radius of the biggest disc centered at $z_0$ which can be embedded in the domain of the function.
The same basic properties hold for differentiable functions in higher complex dimensions. If $\Omega$ is a domain --- i.e., a connected open set --- in $\mathbb{C}^n$, and $f : \Omega \to \mathbb{C}^n$ is once differentiable, then it is in fact analytic, and can be represented as a power series in a neighborhood of any point $z_*$, i.e., we have an expression like
$$f(z) = \sum a_{k_1 \dots k_n} (z_1 - z_*)^{k_1} \dots (z_n - z_*)^{k_n}.$$
The domain in which the series converges is a polydisc, i.e., a product of $n$ discs for each variable individually. A version of Cauchy's integral formula holds for integration over the boundary of a polydisc:
$$f(z) = \frac{1}{(2 \pi i)^{n}} \int d\zeta_1 \dots d\zeta_n \frac{f(\zeta_1, \dots, \zeta_n)}{(\zeta_1 - z_1) \dots (\zeta_n - z_n)}.$$
There is one very important difference between complex analysis in one variable versus complex analysis in several variables, and it is a difference that has remarkable consequences for the structure of quantum field theory. In single-variable complex analysis, many important questions are questions of analytic continuation: given an analytic function $f$ defined in a domain $\Omega,$ does there exist a larger domain $\tilde{\Omega}$ in which $f$ has a unique analytic continuation?
In one variable, this is always a question about the function. In several variables, it is sometimes a question about the domain. More precisely, in $\mathbb{C}^n$ with $n \geq 2,$ there exist pairs of domains $\Omega \subsetneq \tilde{\Omega}$ such that every function $f$ analytic in $\Omega$ admits a unique analytic continuation to $\tilde{\Omega}.$ When this happens, $\tilde{\Omega}$ is called an envelope of holomorphy for $\Omega.$
We will see an explicit example momentarily, but let us first consider the physical consequences of this extraordinary fact. In mathematical approaches to quantum field theory, the fundamental objects of interest are field expectation values in a state $\omega,$
$$\langle \phi(x_1) \dots \phi(x_n) \rangle_{\omega}.$$
In $d$-dimensional Minkowski spacetime, these correlation functions can be thought of as complex-valued functions of $(\mathbb{R}^d)^n.$ (They are in fact distributions, not functions, but this will not be so important for us right now.)
Under certain natural assumptions --- Lorentz invariance and the Hamiltonian being bounded below --- one can often show that the correlation function $\langle \phi(x_1) \dots \phi(x_n) \rangle_\omega$ admits an analytic continuation to some domain in $(\mathbb{C}^d)^n.$ Because of the phenomenon of envelopes of holomorphy, it often suffices to begin with a very modest analytic continuation of the correlation function, then to invoke general principles to show that it must be continuable to a much larger domain. Analytic functions are highly constrained, so simply knowing that correlation functions are analytic in some particular domain is enough to have consequences for the physics of quantum fields.
The purpose of this post is to explain one such physical consequence, which is the timelike tube theorem proved by Borchers. Recently, a generalization due to Strohmaier and Witten has attracted interest due to an apparent connection with bulk reconstruction in holographic quantum gravity. We will content ourselves with the simplest version of the timelike tube theorem, which concerns a timelike segment in two-dimensional Minkowski spacetime with a scalar quantum field. Generalizations to higher-dimensional Minkowski, to more general timelike curves, or to non-scalar fields, are just matters of bookkeeping.
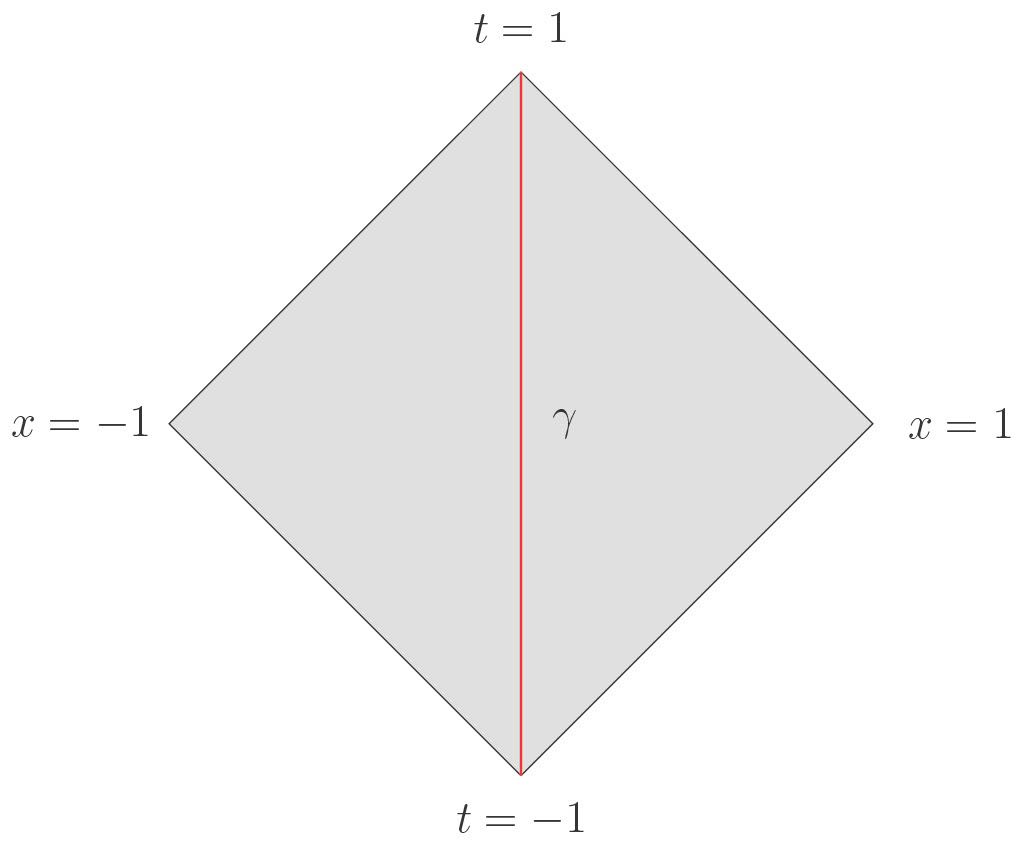
Consider a causal diamond with spatial extent $x \in [-1, 1]$ and time extent $t \in [-1, 1]$, sketched in the figure above. Consider also the vertical timelike segment $x=0, t=[-1, 1],$ which we will call $\gamma.$ The timelike tube theorem says that field operators anywhere in the diamond can be approximated arbitrarily well by field operators in an arbitrarily small neighborhood of $\gamma.$ An equivalent formulation is that if an operator $O$ commutes with every field operator $\phi(x)$ for $x$ in an arbitrarily small neighborhood of $\gamma,$ then $O$ must commute with every field operator $\phi(x)$ in the full causal diamond.
In the rest of this post, we will learn some basic facts about envelopes of holomorphy, then prove the version of the timelike tube theorem explained above. I learned about envelopes of holomorphy from Vladimirov's excellent book (now available from Dover under a slightly different name), and about the timelike tube theorem by plugging Borchers's original German-language paper line-by-line into Google translate.
Prerequisites: Complex analysis and basic quantum field theory.
Table of Contents
- A simple envelope of holomorphy
- The timelike tube theorem
1. A simple envelope of holomorphy
Consider first the annulus domain in $\mathbb{C}$ sketched below, given by $1/2 < |z| < 1.$ Compare it to the filled-in disc $|z| < 1,$ also sketched below. There exist functions analytic in the annulus that cannot be analytically continued to the full disc. An example is the function $f(z) = 1/z,$ which is analytic in the annulus but has no analytic continuation to the disc on account of its singularity at $z=0.$
We will now see that in two complex dimensions, $\mathbb{C}^2,$ the situation is quite different. Every function analytic in the annulus $1/2 < \sqrt{|z_1|^2 + |z_2|^2} < 1$ has a unique analytic continuation to the full ball $\sqrt{|z_1|^2 + |z_2|^2} < 1.$ Let us try to understand why this is the case.
First, given a function $f(z)$ which is analytic in the one-dimensional annulus $1/2 < |z| < 1,$ let us suppose that it does have an analytic continuation to the disc $|z| < 1.$ By Cauchy's integral formula, for $|z| < 3/4,$ the analytic continuation must be given by the contour integral
$$f(z) = \frac{1}{2\pi i} \int_{|\zeta| = 3/4} d\zeta\, \frac{f(\zeta)}{\zeta - z}.$$
Because the contour is inside the annulus, the right-hand side is certainly defined. It is actually not so hard to show, simply by taking a $z$ derivative, that the right-hand side does give an analytic function in $|z| < 3/4,$ and by moving the contour outwards, we can use it to define an analytic function in the full disc $|z| < 1.$ The thing that goes wrong is that this newly defined analytic function is not necessarily an analytic continuation of the original function $f$! For example, given $f(z) = 1/z,$ it is a straightforward exercise to check that the contour integral evaluates to zero everywhere. This is an analytic function in the disc, but it does not continue the function we started with.
In higher dimensions, something very different happens. The basic idea is that we can still use Cauchy's integral formula to figure out what the analytic continuation of $f$ would be if it did exist. But because of some topological magic that happens in higher dimensions, we can also show that the analytic function defined by a contour integral is, in fact, a continuation of the original function.
To see this, let $f(z_1, z_2)$ be analytic in the annulus $1/2 < \sqrt{|z_1|^2 + |z_2|^2} < 1.$
If an analytic continuation exists for the full ball $\sqrt{|z_1|^2 + |z_2|^2} < 1,$ then it must be given by the formula
$$f(z_1, z_2) = \frac{1}{2 \pi i} \int_{\sqrt{|\zeta|^2 + |z_2|^2} = 3/4} d\zeta\, \frac{f(\zeta, z_2)}{\zeta - z_1}.$$
As in the one-complex-dimensional case, it is possible to show that this is an analytic function of $z_1$ and $z_2$ in the full ball, simply by taking derivatives in $z_1$ and $z_2$.
The difference is that for $|z_2| > 1/2,$ not only the circle $\sqrt{|\zeta|^2 + |z|^2} = 3/4$ is in the annulus, but the full filling-in of that circle to a disk is in the annulus. In other words, as we drag the contour around the "hole" in the annulus, eventually its interior is contained in the annulus. Because $f$ is analytic in the annulus, Cauchy's integral formula tells us that the left- and right-hand sides of the above equation agree in this regime. Since these functions are analytic, they agree everywhere, and we have given an explicit formula showing how to analytically continue any function in the annulus to a function in the full ball.
2. The timelike tube theorem
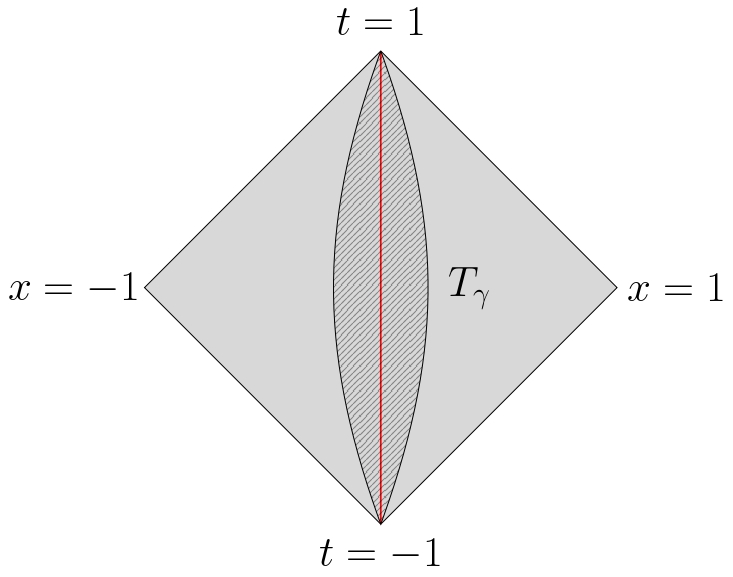
As in the introduction, we consider the causal diamond in two-dimensional Minkowski spacetime sketched below. $\gamma$ is the timelike segment connecting the top and bottom of the diamond, and $T_{\gamma}$ is a small open set containing that segment. Let $O$ be an operator commuting with all fields in the tube, i.e.,
$$O \phi(x) = \phi(x) O, \qquad x \in T_{\gamma}.$$
Our aim is to show that $O$ commutes with every field operator in the full causal diamond.
Let $|\Omega\rangle$ be the vacuum state. Consider the functions on spacetime given by
$$f(x) = \langle \Omega | O \phi(x) | \Omega \rangle$$
and
$$g(x) = \langle \Omega | \phi(x) O | \Omega \rangle.$$
Because of our assumption, we have $f(x) = g(x)$ for $x \in T_{\gamma}.$
In Minkowski spacetime, we have a momentum operator $P_{\mu}$ which acts on fields as $\phi(x + \xi) = e^{i P_{\mu} \xi^{\mu}} \phi(x) e^{- i P_{\mu} \xi^{\mu}}.$ We also have $e^{- i P_{\mu} \xi^{\mu}} |\Omega \rangle = |\Omega \rangle.$ This lets us rewrite $f$ and $g$ as
$$f(x) = \langle \Omega | O e^{i P_{\mu} x^{\mu}} \phi(0) |\Omega \rangle$$
and
$$g(x) = \langle \Omega | \phi(0) e^{- i P_{\mu} x^{\mu}} O |\Omega \rangle.$$
If we assume that energy is bounded below, then we must have $P_{\mu} \xi^{\mu} \geq 0$ for any future-directed $\xi.$ What this tells us is that the expression $e^{- i P_{\mu} x^{\mu}}$ can be analytically continued to complex vectors $z^{\mu}$ so long as the exponential is decaying, i.e., so long as we have $P_{\mu} \text{Im}(z^{\mu}) \leq 0,$ which holds whenever $\text{Im}(z^{\mu})$ is in the past light cone $V^-$. We will shorten this by saying $z^{\mu} \in \mathbb{R}^2 - i V^+.$
From these observations, we conclude that $f(x),$ which is defined on all of spacetime $\mathbb{R}^2$, has an analytic continuation to $\mathbb{R}^2 + i V^+.$ The function $g(x)$ has an analytic continuation to $\mathbb{R}^2 - i V^+.$ Furthermore, we know that $f(x)$ and $g(x)$ agree for a particular open set in $\mathbb{R}^2,$ i.e., for $x \in T_{\gamma}.$
At this point, we may invoke an extraordinary result in multivariable complex analysis called the
edge of the wedge theorem. In single-variable complex analysis, the edge of the wedge theorem says that if a function is analytic in two half-planes and continuous on a segment dividing the half-planes, then the function is in fact analytic in a neighborhood of the segment as well. See the figure below. This isn't so hard to prove using standard results in complex analysis like
Morera's theorem.
The edge-of-the-wedge theorem in higher dimensions is remarkable because it does not require half-spaces; it only requires codimension-0 cones. If $\Gamma \subseteq \mathbb{R}^2$ is some open cone, then any function which is analytic in $\Omega \pm i \Gamma$ and continuous in the limit $\Omega \pm i 0$, is analytic on $\Omega$ as well. This is remarkable, because by expanding in power series around points in $\Omega,$ we may then conclude that the function is analytic in a full complex neighborhood of the real submanifold $\Omega,$ not just in the funny cone domains we started with.
Since our future light cone $V^+$ is certainly an open cone in $\mathbb{R}^2,$ we conclude that our functions $f(x)$ and $g(x)$ are two pieces of a single analytic function $H$ that includes a complex neighborhood of $T_{\gamma}$ within $\mathbb{C}^2.$ We will now show that this function $H$ has a unique analytic continuation to a neighborhood of $D \pm i V^+,$ where $D$ is the full causal diamond containing the timelike curve $\gamma.$ This suffices to prove the theorem, since $f(x) = g(x)$ in $T_{\gamma}$ will then imply $f(x) = g(x)$ in $D$, which implies
$$\langle \Omega | [\phi(x), O] | \Omega \rangle, \qquad x \in D,$$
which implies $[\phi(x), O] = 0$ via standard
Reeh-Schlieder type arguments.
We will now show that the analytic function $H$ built from $f(x)$ and $g(x)$ can be analytically continued to a small complex neighborhood of $D$. We will do this using the same tool as in the toy example of the annulus from the previous section: we will write down a Cauchy-integral formula that defines an analytic function in a neighborhood of $D$ in terms of an integral over values of $H$ in its domain of definition, and which can be shown to agree with $H$ in some neighborhood. For simplicity, we will perform the analytic extension only to the $x \geq 0$ part of the diamond, but the full diamond can be obtained by symmetry.
Every point $(x_0, t_0)$ in the $x \geq 0$ portion of the diamond lies on a unique hyperbola of the form
$$(x - 1)^2 - t^2 = c^2,$$
with
$$c^2 = (x_0 - 1)^2 - t_0^2.$$
These hyperbolas intersect the real axis on the timelike segment $x=0, t=[-1,1]$; see the figure below.
Given one such hyperbola, labeled by the parameter $c \in (0, 1),$ we may parametrize it using a parameter $\zeta$ by
$$x = 1 - c \cosh(\zeta), \quad t = c \sinh(\zeta).$$
The portion of the hyperbola lying in $x \geq 0$ is swept out by real values of $\zeta$ in the regime $|\zeta| \leq \operatorname{arccosh}(1/c).$ But by making $\zeta$ complex, we may extend this hyperbola to some one-dimensional complex submanifold (i.e., two-dimensional real submanifold) of $\mathbb{C}^2.$ The idea is to define the analytic continuation of $H$ at the point $(x, t)$ using a Cauchy integral formula on this complex hyperbola, where the contour of integration lies entirely within the original domain of $H$.
Simple arithmetic shows that for $\text{Im}(\zeta) \neq \pi n,$ the imaginary part of the vector $(x = 1 - c \cosh(\zeta), t = c \sinh(\zeta))$ is timelike, so it lies in the domain of $H$. For $\text{Im}(\zeta) = 0$, we are on the original hyperbola, and we can guarantee that we are in the domain of $H$ so long as we have $\text{Re}(\zeta) = \pm \operatorname{arccosh}(1/c),$ because this is where the hyperbola intersects the timelike segment from which the domain of $H$ was constructed.
This encourages us to consider a contour in the $\zeta$ plane that always lies in $- \pi < \text{Im}(\zeta) < \pi,$ and which intersects the real axis at $\zeta = \pm \operatorname{arccosh}(1/c).$ Any such contour will do; for concreteness, writing $\zeta = \zeta_1 + i \zeta_2,$ we could use the ellipse
$$\frac{\zeta_1}{\operatorname{arccosh}(1/c)^2} + \frac{\zeta_2}{(\pi/2)^2} = 1.$$
We will refer to this contour as $\gamma(c).$
If $H$ is to have an analytic extension to $D$, then for $(x,t) \in D,$ it ought to satisfy the equation
$$H(x, t) = \frac{1}{2 \pi i} \int_{\gamma(c(x, t))} \frac{H\left(1 - c(x,t) \cosh(\zeta), c(x, t) \sinh(\zeta) \right)}{z - \zeta_0(x, t)},$$
with $c(x, t) = \sqrt{(x-1)^2 - t^2}$ defining the hyperbola on which the point $(x, t)$ lies, and $\zeta_0(x, t) = \operatorname{arcsinh}(t/c(x,t))$ giving the value of $\zeta$ at which the hyperbola passes through $(x, t).$
$\zeta_0$ and $c$ are analytic functions of $(x, t) \in D$, so they can be extended to a small complex neighborhood of $D$. For complex variables $u = x + i \chi, v = t + i \tau,$ this gives a function
$$H(u, v) = \frac{1}{2\pi i} \int_{\gamma(c(u, v))} \frac{H \left(1 - c(u, v) \cosh(\zeta), c(u, v) \sinh(\zeta)\right)}{z - \zeta_0(u, v)}$$
defined in a small complex neighborhood of $D$. Simply by differentiating, and using the continuous dependence of $c$ and $\zeta_0$ on $(u, v)$, it is easy to show that $H$ is analytic. For $u$ and $v$ sufficiently close to the timelike segment $x=0, t=[-1, 1]$ the interior of the curve $\gamma(c(u, v))$ will lie entirely within the domain of holomorphy of $H$, so the integral expression agrees with the original value of $H$, in that domain, and therefore furnishes an analytic continuation of $H$.




Comments
Post a Comment